Quantum-Safe Cryptography—Surviving the Upcoming Quantum Cryptographic Apocalypse


The sky is indeed falling, at least for those of us concerned about computer and information security. The fundamental cryptographic algorithms now widely used to protect every facet of digital life will, within several years, be easily defeated by quantum computers. These algorithms touch every aspect of our daily lives, from online shopping and credit card transactions, to validating passports and ID badge systems, and even managing the control systems powering the electric grid.

Labeled as the ‘Quantum Cryptographic Apocalypse,’ this imminent point is the inevitable day when quantum computing renders existing de facto cryptographic techniques obsolete. Specifically, the RSA and ECC encryption algorithms that are fundamental to our modern security, communication and identification systems will be vulnerable to attacks from quantum computers.
The good news, however, is that it is not too late to avert this crisis. Efforts are currently underway to implement new, quantum safe crypto algorithms. The Quantum Cryptographic Apocalypse will require a complete retooling of PKI systems throughout all aspects of industry to use these new crypto algorithms. Doing so will keep our digital systems safe and functional.
Encryption
Before diving into the details about how quantum computers will break our existing security systems, lets first talk about what encryption is and how it works.
Encryption is the process of converting data, known as plaintext, from a readable format to an encoded format known as cyphertext. Cyphertext cannot be read without decrypting the data to return it to its original plaintext format. The encryption process relies on an encryption key, that must be kept secret.
To put it extremely simply, encryption effectively protects data because the computing tasks of encryption and decrypting data are relatively easy, but breaking an encryption system is very, very hard. That is to say, it is very difficult to discover the encryption key by a brute force attack.
An attacker cannot decrypt data without the encryption keys, so they will often attempt to discover or steal the encryption key(s). If the hacker cannot find a way to steal the keys, they can attempt a “brute force” attack in which they try all possible encryption keys. With the encryption algorithms being used today, a hacker cannot discover the keys and decrypt data that has been encrypted without huge amounts of processing time, even if the attacker knows the encryption algorithm that was used. For RSA-2048, current computers would take around 300 trillion years to discover RSA keys using a brute force attack.
As computing power has increased, cryptographic implementations have used longer key lengths to deliver encryption solutions that continue to provide robust security. However, as computing power for both users of encryption and attackers are increasing at a similar rate, the overall security of these systems remains strong, provided longer key lengths have been implemented.
When we discuss encryption, it is important to note that there are two types of encryption commonly used in most security systems.
Asymmetric vs. Symmetric Encryption
Most security protocols and systems employ both symmetric and asymmetric encryption. For example, the Transport Layer Security protocol (TLS) uses asymmetric encryption to securely exchange a secret symmetric key at the start of a session. Subsequently, TLS transitions to symmetric encryption using the secret key established during the key-exchange process.
Symmetric Encryption
Symmetric encryption is conceptually straightforward. It uses a single secret key that is shared by both communicating entities (see Figure 1).
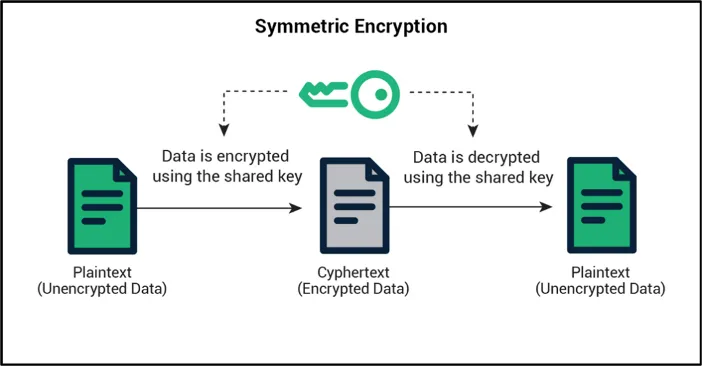
The problem, of course, is how can keys be exchanged without someone or something intercepting them? That is where asymmetric encryption comes into play, by allowing the symmetric encryption key to be securely exchanged.
Asymmetric encryption
Asymmetric encryption uses a key pair consisting of a public key and a private key (see Figure 2). Each node has its own key pair. The private key must be kept secret, but the public key can be shared with other nodes.
Key pairs are created in such a way that data encrypted with a public key can be decrypted only with the correct private key, and vice versa. If Device A wants to send data to Device B, then Device A can encrypt that data using Device B’s public key. That data can only be decrypted using Device B’s private key. Only Device B knows the private key, so only Device B can decrypt the message.
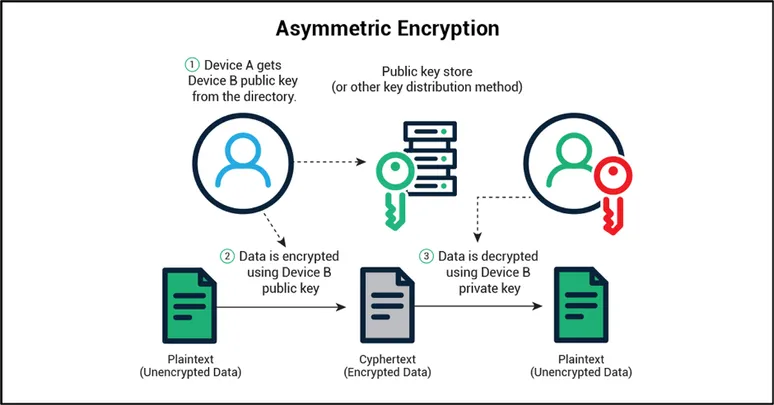
All key-pairs are mathematically related to enable encryption/decryption in this manner. It is critical that only the public keys are exchanged and that the private keys are never exchanged. The mathematical relationship between the public and private keys ensures that data encrypted with the public key can only be decrypted with the corresponding private key; that is, it can be decoded only with the intended receiver’s private key.
A major shortcoming of asymmetric encryption is that it can easily use 100x more CPU cycles than symmetric encryption. This processing load causes problems for any system, and worse for embedded devices that perform time-sensitive operations and/or have limited system resources. The solution is to first run an asymmetric session only to create an initial encrypted connection for exchanging a secret symmetric key. Thereafter, that symmetric key is used for the remainder of the communication session.
PKI, Certificates and Encryption
Public Key Infrastructure (PKI) systems provide the foundation for identity and security for virtually all modern computing systems. Basic Internet functionality, IoT Security, Credit and Debit Card transactions, and even modern ID systems including passports, all depend on PKI and the digital certificates issued by PKI systems.
Digital certificates utilize asymmetric encryption in which the public key is published to enable authentication of the user or device holding the corresponding private key. Certificates, much like drivers’ licenses, provide an identity for the key holder. In other words, the certificate includes information about who should be using the key. This identity could be a website domain (such as sectigo.com), the device ID of an IoT device, or an email address.
Properties of RSA and ECC keys
With RSA, the public key is a larger integer created from two large prime numbers. These prime numbers also form the basis of the private key. Because of the way traditional computers work, factoring prime numbers is tremendously difficult as the computer has no choice but to go through every combination. That is the basis of RSA encryption; the private key cannot be derived from the public key in a reasonable amount of time because factoring prime numbers is very computationally expensive.
Elliptic Curve Cryptography works because of the properties of an elliptic curve and solving for two points in that curve is exceedingly difficult for a traditional computer. As such, it is almost impossible to derive the private key from the public key, rendering brute force attacks on these crypto systems ineffective.
With Quantum Computing, these fundamental underlying assumptions upon which our entire security architecture are built are no longer true. Quantum computers can derive the private key from a public key in a reasonable amount of time.
Quantum Computing and Code Breaking
Quantum computers operate in fundamentally different ways than traditional computers. Unlike traditional computers, where all information is stored as a traditional bit of data that is either zero or one, quantum computers operate using a qubit (or a quantum bit). The qubit can be zero or one, but can also represent some super position of that, and, interestingly enough, can become entangled and even interfere with one another.
Qubits have very interesting properties that make solving some computing problems drastically easier. By using quantum computing, factoring exceptionally large prime numbers suddenly becomes computationally feasible. With quantum computers, not only is encryption easy, but breaking traditional asymmetric encryption algorithms is also easy.
Interestingly, symmetric encryption algorithms and hash algorithms are not currently threatened by quantum computing and do not need to be replaced. Breaking asymmetric encryption threatens most encryption systems that rely on asymmetric encryption to establish keys for symmetric encryption operations. The focus of quantum-safe encryption is on replacing the asymmetric encryption algorithms used for key exchange and digital signature operations.
The Looming Quantum Apocalypse – When Do We Need to Worry?
The Quantum Apocalypse is the time at which quantum computing reaches a level of practicality where decryption capabilities are vastly improved and the parity between encrypting and breaking encryption is no longer present. In other words, the point in time when the disparity in the amount of processing power required to break encryption is no longer so extreme that it becomes possible for bad guys to start to decrypt our encrypted data in a short enough timeframe to be practical.
When we talk about the Quantum Apocalypse, the million-dollar question, of course, is when will this take place? Michele Mosca, a co-founder of the Institute for Quantum Computing, provided a framework for evaluating when this will happen and for determining our readiness.
Mosca’s inequality is X + Y >? Z.

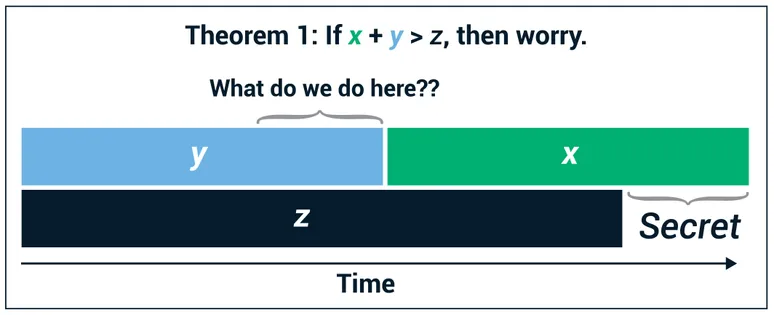
In other words, is X + Y greater than Z? In this equation, X is how long do you need your crypto keys to be secure. In other words, what is the security shelf life? Y is how long will it take to retool security systems to adopt quantum-safe crypto algorithms, or what is your migration time? And Z is how long it will take for large scale quantum computing to be built. In other words, that is the collapse time.
The challenge is that X, Y and Z are all uncertain and, in fact, vary from system to system.
Let’s look at each of these in turn.
X is how long security keys, or more precisely the data encrypted with those keys, must be protected. This is obviously application dependent. For an IoT sensor system in which data is collected, used to make real-time decisions, and then discarded, X may be minutes, days or at most, weeks.
For transactions between my laptop and my online banking system, in which my password is exchanged, X is the length of time until I change my password. For most users, this is a period of a year or perhaps a few years. Good password hygiene practices can reduce this period, but the information exchanged would also include personal financial information that would likely have a shelf life of a few years. Other information, such as communication of trade secrets, classified government documents or other highly sensitive data may have a shelf life of decades. The great variability of X does significantly complicate the evaluation of Mosca’s inequality to determine when the pending Quantum Apocalypse will occur.
Y, as stated earlier, is the length of time required to retool security systems to utilize quantum-safe crypto algorithms.
This is itself a complex topic and will be covered in more detail in another white paper, but this element of the process can be broken down into two sub categories: the time required to develop quantum safe crypto algorithms and the time required to transition our systems to utilize these algorithms.
NIST has been leading a process to develop and vet a set of quantum-safe crypto algorithms. This process began in 2016 and is expected to be completed in the 2022/2024 timeframe. As of January 2019, NIST had identified 26 candidate algorithms that were proceeding to the 2nd round of the process.
In addition to the time to develop the algorithms, we must consider the time to update existing PKI systems and all the enterprise, IoT, automation, web services, and other identity systems that utilize crypto algorithms. Many of these systems are complex and updating them is no simple task. On the extremely low end, timeframes will vary from several months to several years for complex systems with multiple components and dependencies.
There is a bit of good news in this as we do not need to wait until NIST finishes its process to begin retooling our systems. These processes can occur in parallel using NIST candidate algorithms. Furthermore, certificate renewal automation solutions and implementing “crypto agility”, (the ability to migrate to new crypto algorithms as they become available), can help ease the eventual burden of migrating to new crypto algorithms.
Finally, Z is the time required to for a sufficiently powerful quantum computer to be developed that can defeat existing crypto solutions in a reasonable amount of time.
What does breaking RSA 2048 in a “reasonable amount of time” actually mean?
This does not mean doing real-time decryption of an TLS encrypted stream of information. Achieving real-time decryption of a TLS stream would require defeating the TLS key arrangements with Diffie-Hellman. This would require intercepting the key-exchange messages, breaking the encryption key, reading the encrypted stream, and decrypting it in real time.
The bigger threat is an attacker recording the data stream and being able to retroactively decrypt it within a reasonable amount of time. In this context, a reasonable amount of time can mean a month or two instead of lifetimes, as it would be with current computing systems.
As we look at this an important fact to keep in mind is that quantum computers do not affect all cryptography in the same way. Symmetric encryption algorithms such as AES and hash algorithms such as SHA hashing algorithm are not susceptible to quantum attacks. These algorithms are quantum-safe just by their methods of operating; they are not susceptible to Shor’s algorithm. Quantum computing might warrant the need for hashing algorithms to utilize a larger number of bits, but fundamentally they are not broken by quantum computers.
Shor’s Algorithm
As discussed earlier, RSA is exceedingly difficult to break because factoring prime numbers with traditional computers is very, very hard. It would take a modern computer trillions of years to break an RSA-2048 key.
However, with quantum computers, the game changes. Peter Shor developed Shor’s algorithm back in 1994/1995. The algorithm provides a geometric method of finding prime factors of a given integer. Shor’s algorithm operates by finding periodicities within a function and works because primes tend to follow a pattern or a sequence. Shor’s algorithm can be implemented efficiently with a quantum computer and is, therefore, what would be used to break the RSA encryption technique once quantum computers are sufficiently powerful.
When protecting against attacks by traditional computers, systems can achieve great security by extending the key-length of the algorithm. An organization could switch to RSA 4096, for example. With quantum computers, however, that approach will not work. Even though RSA 4096 uses a key that is twice as long, the difference in time for a quantum computer to break RSA 4096 vs. RSA 2048 is negligible. A fundamentally different encryption algorithm is required to provide security against quantum computing attacks.
If we look at the details, most experts agree that it currently takes about 5,000 to 10,000 qubits to solve RSA 2048 in what we are calling a “reasonable” amount of time. As of 2020, state-of-the-art quantum computers have achieved about 50 qubits for general purpose quantum computers, while quantum annealing machines like the D-Wave computers have achieved much larger numbers of qubits. In addition, in 2020, the D-Wave machine has achieved 2000 qubits, but this is not a universal quantum computer and has no error correct. As a result, the qubits are easier to build, but a substantial amount of error correction is required.
Estimates vary, but the number of “universal qubits” achieved by the D-Wave machine after error correction range from 10% to 0.1% of the number of physical cubits, so the D-Wave machine is the equivalent to anywhere from 2 to 200 cubits from a general purpose quantum computer.
Researchers like Michele Mosca, from the University of Waterloo, are predicting that the rate at which quantum computing is advancing will continue to accelerate and that we will get from 50 qubits today to 500 qubits, to 1,000 qubits, to 5,000 qubits, to 10,000 qubits, in a fairly linear progression.
And it is then, when we achieve 5,000 to 10,000 qubits, that current crypto algorithms will be broken.
Predictions on time vary, but most experts agree that quantum computers will break RSA encryption somewhere in the timeframe of 2026 to 2031.
Summary
If we look back at Mosca’s inequality, and then factor in that some data must be protected for decades, we have then already passed the Quantum Apocalypse date for some use cases.
For most systems, there is still time to develop solutions, but 2026 is extremely close. Six years to swap out our entire complex infrastructure is a Herculean task, especially since quantum-safe crypto algorithms will not be standardized for several more years.
This is an all-hands-on-deck kind of situation.
The crisis cannot be ignored. Everyone in the industry needs to be thinking about quantum-safe cryptography. As a trusted third-party CA, Sectigo is currently investing in creating quantum-safe PKI solutions to enable users of PKI to begin the task of migrating to newer quantum-safe crypto algorithms.
This is a complex topic, and we are going to be providing a series of resources to help our customers understand the problem and to develop solutions. At Sectigo Quantum Labs, we are working with industry leaders to develop solutions to enable migration to new algorithms and ensure our customers are prepared for the Quantum Apocalypse.